Los sólidos Platónicos son considerados las formas de los componentes fundamentales del Universo físico

Los cinco poliedros regulares fueron descubiertos por los antiguos griegos, los pitagóricos conocían el tetraedro, el cubo y el dodecaedro, el matemático Teeteto añadió el octaedro y el icosaedro, estas formas se llaman también los sólidos platónicos, después el antiguo filósofo griego Platón; Platón, que respeta en gran medida el trabajo de Teeteto, especuló que estos cinco sólidos eran las formas de los componentes fundamentales del universo físico.
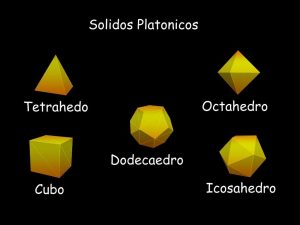
Sólo hay cinco sólidos geométricos que se pueden hacer usando un polígono regular y tener el mismo número de estos polígonos se reúnen en cada esquina. Los cinco sólidos platónicos o poliedros regulares son el tetraedro, cubo, octaedro, dodecaedro e icosaedro.
Los sólidos platónicos, también llamados los sólidos regulares o poliedros regulares, son poliedros convexos con caras equivalentes compuestas de polígonos regulares convexos congruentes, como ya se nombro previamente hay exactamente cinco de tales sólidos ellos son el cubo, el dodecaedro, el icosaedro, el octaedro y el tetraedro, como fue demostrado por Euclides en la última propuesta de los Elementos.
Los sólidos platónicos son a veces también llamadas figuras cósmicas, aunque este término se utiliza a veces para referirse colectivamente tanto a los sólidos platónicos y a los sólidos de Kepler Poinsot.
Los sólidos platónicos eran conocidos por los antiguos griegos, y fueron descritos por Platón en su Timeo ca. 350 antes de Cristo, en esta obra, Platón equipara el tetraedro con el elemento fuego, el icosaedro con agua, el cubo con la tierra, el octaedro con el aire y el dodecaedro con la materia de la que se hicieron las constelaciones y los cielos.

Anterior a Platón, la población prehistórica de Escocia desarrolló los cinco sólidos mil años antes, los modelos de piedra se conservan en el Museo Ashmolean de Oxford.
Los Sólidos Platónicos, también llamados los Sólidos Regulares o Poliedros Regulares, son Poliedros Convexos con Caras Equivalentes
Schläfli demostró que hay exactamente seis cuerpos regulares con propiedades platónicas es decir, politopos regulares en cuatro dimensiones, tres de cada cinco dimensiones y tres en todas las dimensiones superiores, sin embargo, mantuvo su trabajo que no contenía ilustraciones prácticamente desconocido hasta que fue publicado parcialmente en Inglés por Cayley.
Otros matemáticos como Stringham posteriormente descubrieron resultados similares de forma independiente en 1880 y la obra de Schläfli se publicó póstumamente en su totalidad en 1901.
Si P es un poliedro con congruentes convexos caras poligonales regulares, entonces Cromwell muestra que las siguientes afirmaciones son equivalentes.
1. Los vértices de P todos se encuentran en una esfera.
2. Todos los ángulos diedros son iguales.
3. Todas las figuras son de vértices de polígonos regulares.
4. Todos los ángulos sólidos son equivalentes.
5. Todos los vértices están rodeados por el mismo número de caras.
Sea v, a veces denotado n_0 ser el número de vértices del poliedro, e el número de aristas y f el número de caras, el número de vértices v, bordes de correo y se enfrenta a f y los grupos de puntos de los sólidos platónicos.
El número ordenada de las caras de los sólidos platónicos son 4, 6, 8, 12, 20; en el tetraedro , cubo, octaedro, dodecaedro, icosaedro, que es también el número ordenado de vértices en el tetraedro pedido , octaedro, cubo, icosaedro, dodecaedro.
Los duales de los sólidos platónicos son otros sólidos platónicos y de hecho, el dual del tetraedro es otro tetraedro, deje r_d ser el radio del poliedro dual correspondiente a la esfera que toca las caras del sólido dual, h sea el midradius tanto del poliedro y su dual correspondiente a la esfera, que toca los bordes de tanto el poliedro y sus duales, R la circunradio correspondiente a la circumesfera del sólido que toca los vértices del sólido de la platónica sólido y una longitud del borde del sólido.




