La estructura fractal de los osciladores armónicos en la música: Concierto de año nuevo: JS.Bach. Conciertos de Brandemburgo.

El análisis de la estructura de diferentes obras musicales ha demostrado que la selección de las notas que han hecho diferentes compositores, en distintas épocas, tiene algunos elementos comunes. Trátese de uno de los Conciertos de Brandemburgo de Bach, del Cuarteto de cuerdas # 3 de Babbit, de obras de piano de Scott Joplin, todas estas obras tienen la misma forma si se considera la estructura en términos de frecuencias. Explicaremos esto a continuación.

En el análisis auditivo de diversas obras musicales una cantidad que se ha estudiado es la potencia de audio de la música. Esta cantidad es, en esencia, la energía que se emite en forma de ondas sonoras cada segundo, cuando se ejecuta la obra musical. Al analizar cómo está estructurada esta cantidad, en términos de la frecuencia, se obtiene lo que se llama su espectro.

¿Cómo dependen de la frecuencia los espectros de las diferentes obras musicales?

Los análisis hechos de diferentes obras musicales han mostrado que sus espectros dependen de la frecuencia, que llamaremos con la letra f, como (1 /f). Si recordamos lo que se analizó en el capítulo anterior vemos que este espectro es una ley de potencia que, en el lenguaje matemático, depende de la frecuencia en forma inversa a la primera potencia de f (ya que el exponente de la f en (1 /f) es 1). Por lo tanto, como ya se describió, este espectro es autosimilar y en consecuencia, contiene una estructura fractal.

Un espectro del tipo mencionado en el párrafo anterior recibe el nombre de espectro rosa.

¿Por qué Bach y muchos otros compositores escogieron el espectro rosa? La realidad es que ningún músico oyó hablar jamás de estas ideas, ni mucho menos las escogió de manera deliberada. Para entender lo que sucede explicaremos cómo se haría música con otro tipo de espectro.

Una forma sería como sigue: cada nota que se escribe es tal que su posición y duración no dependen para nada de las notas anteriores ni de su duración. En este caso se dice que la composición es completamente al azar o estocástica. Un ejemplo de este tipo de música se presenta en la figura 33(a). El espectro de la potencia de audio de este tipo de música es el mismo para cualquier valor de la frecuencia, lo que significa que el valor de la potencia es el mismo para cualesquiera valores de la frecuencia, o sea, que se trata de una cantidad constante. Matemáticamente, el espectro depende de la frecuencia (1/f0), ya que f0 = 1. A un espectro de este tipo se le llama blanco. Si se tocara este tipo de música en un instrumento la oiríamos sin estructura; además daría la impresión de que de una nota a otra siempre habría una sorpresa.

Otro tipo de espectro, yéndose al otro extremo, es el que depende de la frecuencia (1/f²), espectro llamado brown o café, nombre que se le dio porque está asociado al movimiento browniano que se trató en el capítulo IV. En la figura 33(b) se presenta música que tiene el espectro café. En la música cada nota y su duración dependen en grado considerable de las notas anteriores. Por lo tanto, la sensación que se tiene al escucharla es que después de haber tocado unas notas las que siguen son previsibles.

En la figura: (a) Ejemplo de música blanca. (b) Ejemplo de música café. (c) Ejemplo de música rosa.

La música que tiene espectro rosa, o sea (1/f), se encuentra, por así decirlo, entre los casos de música al azar (espectro blanco) y música determinista (espectro café). En este caso las notas y su duración no son ni muy previsibles ni muy sorprendentes. Un ejemplo de este tipo de música se muestra en la figura 33(c).

Regresando a la pregunta que se hizo arriba: ¿por qué los compositores usaron efectivamente espectros rosas, o sea una ley de potencias (1/f) para componer su música?, se puede afirmar que los compositores han intentado, y por cierto muchos de ellos logrado, componer música interesante. La cuestión se debería plantear como sigue: ¿por qué la música interesante tiene un espectro rosa? La respuesta podría ser que la música con este tipo de espectro resulta ser ni muy previsible (espectro café) ni muy sorprendente (espectro blanco). El científico holandés Balthazaar van de Pol afirmó en una ocasión que la música de Bach es grandiosa porque es inevitable y al mismo tiempo sorprendente, lo que significa que su espectro es rosa.

Debido a que la música que tiene un espectro rosa es autosimilar, tiene estructura similar en diferentes escalas de frecuencias. Lo que ocurre en una escala de frecuencias debe ocurrir en cualquier otra escala de frecuencias. Si se grabara una composición de este tipo en cinta magnética a cierta velocidad y se tocara a distintas velocidades, lo que se oiría sería similar a lo grabado. Esto contrasta con lo que ocurre con la voz humana, pues cuando se toca una grabación a una velocidad, por ejemplo al doble de lo que debiera hacerse, se oye muy chillona. Una forma de exhibir la autosimilitud es con ayuda de un aparato electrónico que genere sonidos de las frecuencias que uno desea. Si se produce un sonido que sea la superposición de 2 notas, siendo cada nota una octava (de frecuencia doble) de la anterior y se empieza con una nota de 10 Hertz (Hz), (1 hertz = 1Hz = 1/seg), las siguientes 11 notas serían de frecuencias:

20 = 2 x l0, 40 = 4 x10, 80 = 8 x 10, 160 =16 x 10,

320 = 32 x 10, 640 = 64 x 10, 1280 = 128 x 10,

2560 = 256 x 10, 5120 = 5l2 x l0, 10 240 =1024 x 10 y

20 480 = 2 048 x 10, todas en unidades Hz.

Ahora cambiemos cada una de estas notas por otras que sean de frecuencias mayores por un semitono (que corresponde a la diferencia entre dos notas sucesivas de un piano); la frecuencia del semitono se obtiene de la nota anterior multiplicando por 1.05946. Ahora se tocará el sonido que es la superposición de las frecuencias siguientes:

10 x 1.0594 = 10.6, 20 x 1.05946 = 21.2,

40 x 1.05946 = 42.38, 80 x 1.05946 = 84.76,

160 x 1.05946 = 169.51, 320 x 1.05946 = 339.03,

640 x 1.05946 = 678.06, 1 280 x 1.05946 = 1356.11,

2560x 1.05946 = 2712.22, 5120 x 1.05946 = 5424.44,

10240 x 1.05946 = 10848.88 y 20480 x 1.05946 = 21697.74 Hz

Este sonido se oirá con un tono más alto que el anterior.

Si se aumenta otra vez la frecuencia de cada una de las notas en un semitono, la superposición de los nuevos sonidos producirá un sonido de tono aún más alto. Si se repite 12 veces el proceso de aumentar en un semitono cada uno de los componentes del sonido, resulta que el sonido que se produce es ¡indistinguible del original! Ésta es una demostración musical de la autosimilitud.

Adicionalmente, si tomamos como referencia los diagramas de tiempo/espectro no audible, tendremos que en los matices >20 Hz y superiores a 28.000 Hz, obtendremos un logaritmo armónico que se expresa como una sucesión de eventos simples y dobles en los silencios:

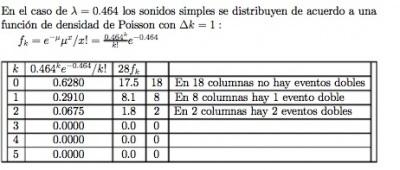
La clave de los osciladores armónicos está en la sucesión de silencios o cadenas de frecuencias del espectro no audible.

La combinación de los conceptos anteriores, da como resultado esta maravilla que les ofrecemos para recibir el nuevo año 2011: